Method Dispatch

When a generic function is called, the generic function uses the classes and identities of the arguments to determine which methods to call. This process is called method dispatch.

Method dispatch occurs in three phases. First, all the applicable methods are selected. Next, the applicable methods are sorted by specificity. Then the most specific method is called.

Method specificity[17]

This section covers how methods are sorted by specificity.

For any two methods A and B that are applicable to a given generic function call, one method may be more specific than the other, or the methods may be ambiguous methods.

To order two methods A and B with respect to a particular set of arguments, compare each of A's specializers with B's specializer in the corresponding position using the corresponding argument. The comparison works in the following way.

• If the specializers are type equivalent, then A and B are unordered at the current argument position. That is, this argument position provides no information about the order of the two methods.
• Otherwise, if the specializer of A is a subtype of the specializer of B, then A precedes B at the current argument position. Similarly, B precedes A at this position if B's specializer is a subtype of A's specializer.
• Otherwise, if both specializers are classes, then their order in the class precedence list of the argument's class is used to determine which is more specific. (See the next section, Computing the Class Precedence List, for more detail.) If A's specializer precedes B's specializer in the class precedence list of the argument's class, then A precedes B at the current argument position. Similarly, B precedes A at this position if B's specializer precedes A's in the class precedence list of the argument's class.
• Otherwise, the methods are ambiguous methods.

The method A is more specific than the method B if and only if A precedes B or is unordered with respect to B in all required argument positions, and precedes B in at least one argument position. Similarly, B is more specific than A if and only if B precedes A or is unordered with respect to A in all required argument positions, and precedes A in at least one argument position. If neither of these cases apply, i.e. neither method is more specific than the other, then A and B are ambiguous methods.

When the applicable methods are sorted by specificity, the sorted list is divided into two parts, each possibly empty. The first part contains methods that are more specific than every method that follows them. The second part (which cannot be sorted itself) begins at the first point of ambiguity; there are at least two methods that could equally well go first in the second part. If the first part is empty, generic function dispatch signals an "ambiguous method" error. If the last method in the first part calls next-method, the call signals an "ambiguous next method" error.

Examples of method specificity

Consider the following class definitions

define class <sentient> (<life-form>) ... end class;
define class <bipedal> (<life-form>) ... end class;
define class <intelligent> (<sentient>) ... end class;
define class <humanoid> (<bipedal>) ... end class;
define class <vulcan> (<intelligent>, <humanoid>) ... end class;

which form the class relationships shown in the following graph: 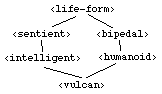Computing the class precedence list for <vulcan> yields

(<vulcan>,<intelligent>,<sentient>,<humanoid>,<bipedal>,<life-form>)

In this class precedence list, note that classes in the simple superclass chains (<intelligent>,<sentient>) and (<humanoid>,<bipedal>) are kept adjacent.

The class precedence lists computed for two different classes may have different precedence orders for some intermediate superclasses. This is not a problem as long as there is no class which inherits from both classes. For example, we could define a class <human> as follows:

define class <human> (<humanoid>, <intelligent>) ... end class;

For the class <human> defined as above, the class precedence list would be

(<human>,<humanoid>,<bipedal>,<intelligent>,<sentientgt;,<life-form>)

It is not a problem that the two class precedence lists give different orders to some of the intermediate superclasses such as <bipedal> and <sentient> as long as no class is added which inherits from both <vulcan> and <human>.

When sorting the applicable methods, each specializer pair needs to be compared with respect to the class precedence list for the class of the argument passed to the generic function in that argument position, because the class precedence list might be different depending on which class it was computed from. For example, given the following definitions

define class <vulcan> (<intelligent>, <humanoid>) end class;
define class <human> (<humanoid>, <intelligent>) end class;
define method psychoanalyze (being :: <intelligent>) ... 
   end method;
define method psychoanalyze (being :: <humanoid>) ... 
   end method;

calling the generic function psychoanalyze on a being of type <human> would cause the method for <humanoid> to be called first, while calling the generic function on a being of type <vulcan> would cause the method for <intelligent> to be called first.

There is no reference to lexicographic order in sorting multimethods.[18] Given the above class definitions, the following methods are unambiguous when superior-being is called on two beings of type <vulcan> or two beings of type <human>, but the methods are ambiguous when superior-being is called on a being of type <vulcan> and a being of type <human> (because it is ambiguous whether to choose the most-intelligent-being, or the best-looking-being):

define method superior-being (a :: <intelligent>,
                              b :: <intelligent>) 
  most-intelligent-being (a, b)
  end method;

define method superior-being (a :: <humanoid>,
                              b :: <humanoid>)
  best-looking-being (a, b)
  end method;

Computing the Class Precedence List[19]

The definition of a class specifies a total ordering on that class and its direct superclasses. This ordering is called the local precedence order. In the local precedence order, the class precedes its direct superclasses, and each direct superclass precedes all other direct superclasses following it in the sequence of direct superclasses of the class definition.

The class precedence list for a class C is a total ordering on C and its superclasses that is consistent with the local precedence orders for each of C and its superclasses.

Sometimes there are several possible total orderings on C and its superclasses that are consistent with the local precedence orders for each of C and its superclasses. Dylan uses a deterministic algorithm to compute the class precedence list, which chooses one of the possible total orderings. The algorithm has the effect that the classes in a simple superclass chain are adjacent in the class precedence list, and classes in each relatively separated subgraph are adjacent in the class precedence list.

Sometimes there is no possible total ordering on C and its superclasses that is consistent with the local precedence orders for each of C and its superclasses. In this case, the class precedence list cannot be computed, and Dylan signals an error.

To compute the class precedence list:

Let S be the set of C and all of its superclasses.

For each class c in S, let

Rc = {(c, c1), (c1, c2), .... , (cn-1, cn)}

where c1 ,..., cn are the direct superclasses of c in the order in which they are mentioned in the class definition for c.

Let R be the union of all Rc for every class c in S. The set R might or might not generate a partial ordering, depending on whether the Rc are consistent; it is assumed that they are consistent and that R generates a partial ordering. When the Rc are not consistent, it is said that R is inconsistent.

To compute the class precedence list for C, topologically sort C and its superclasses with respect to R. Topological sorting proceeds in the following way:

• Find a class N in S such that no other class precedes N according to the elements in R.
• If there are several classes from S with no predecessors, select the one that has a direct subclass rightmost in the partial class precedence list computed so far. In more precise terms, let {N1,...Nm}, m>=2, be the classes from S with no predecessors. Let (C1,...,Cn), n>=1, be the partial class precedence list computed so far. C1 is the most specific class, and Cn is the least specific. Let 1<=j<=n be the largest number such that there exists an i where 1<=i<=m and Ni is a direct superclass of Cj. Select Ni.
• Place N first in the result. Remove N from S, and remove all pairs of the form (N, M), such that M is an element of S, from R.
• Repeat the process, adding classes with no predecessors to the end of the result. Stop when no element can be found that has no predecessor.

If S is not empty and the process has stopped, R is inconsistent because it contains a loop. That is, there is a chain of classes C1,....,Cn in S such that Ci precedes Ci+1, 1<=i<n, and Cn precedes C1. When R is inconsistent, there is no possible total ordering on C and its superclasses that is consistent with the local precedence orders for each of C and its superclasses, and an error is signaled.

Calling More General Methods

In many situations, a subclass wants to modify the behavior of a method, rather than replace it completely; it wants to perform some work but also use the inherited behavior. This can be accomplished with next-method. next-method is a function that, when called, invokes the next most specific method applicable in the generic function. The next-method is the value of the #next parameter. Normally this parameter is named next-method, though it can have other names at the programmer's discretion.

In the following example, the double method for <float> prints out a notice and then calls next-method, which invokes the next most specific method, in this case the method for <number>.[20]

? define method double (num :: <float>)
    print("doubling a floating-point number")
    next-method()
  end method;

? double(10.5)
doubling a floating-point number
21.0

If there are no more methods available, the next-method parameter will be bound to the value #f instead of to a method.

Passing Different Arguments to Next-Method

In the usual case, next-method is called with no arguments. This indicates that the next-method should be passed the same arguments that were supplied to the current method.

It is valid to supply arguments, including different arguments, when calling next-method. However, if you pass different arguments, the new arguments must result in the same ordered sequence of applicable methods, in the same order, as the original arguments. Otherwise, the behavior of Dylan is undefined.

In some cases, the methods in a generic function accept different keyword arguments. In such cases, it's convenient for the methods also to accept a rest parameter. That way, all the non-required arguments to the generic function are captured in the rest parameter. By using apply, the next-method can be invoked with the complete set of arguments.

The Next-Method Parameter

The next-method parameter is passed behind the scenes. When a method is called by its generic function, the generic function dispatch mechanism automatically passes the appropriate value for next-method. There is no way for a user program to specify the next-method argument when calling a method.

If you create a method directly (i.e., with method rather than with define method) and you want this method to accept a next-method parameter, then you should insert a #next into the parameter list explicitly. You would do this if you are creating a method that you plan to add to a generic function, and you want this method to be able to call next-method. You can also supply the next-method parameter when using define method, in cases where you want to give the parameter a different name.